定义
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
算法思路
归并排序算法有两个基本的操作,一个是分,也就是把原数组划分成两个子数组的过程。另一个是治,它将两个有序数组合并成一个更大的有序数组。
- 将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。1. 将子表两两合并,每合并一次,就会产生一个新的且更长的有序表,重复这一步骤,直到最后只剩下一个子表,这个子表就是排好序的线性表。
图解算法
假设我们有一个初始数列为{8, 4, 5, 7, 1, 3, 6, 2},整个归并排序的过程如下图所示。
分而治之
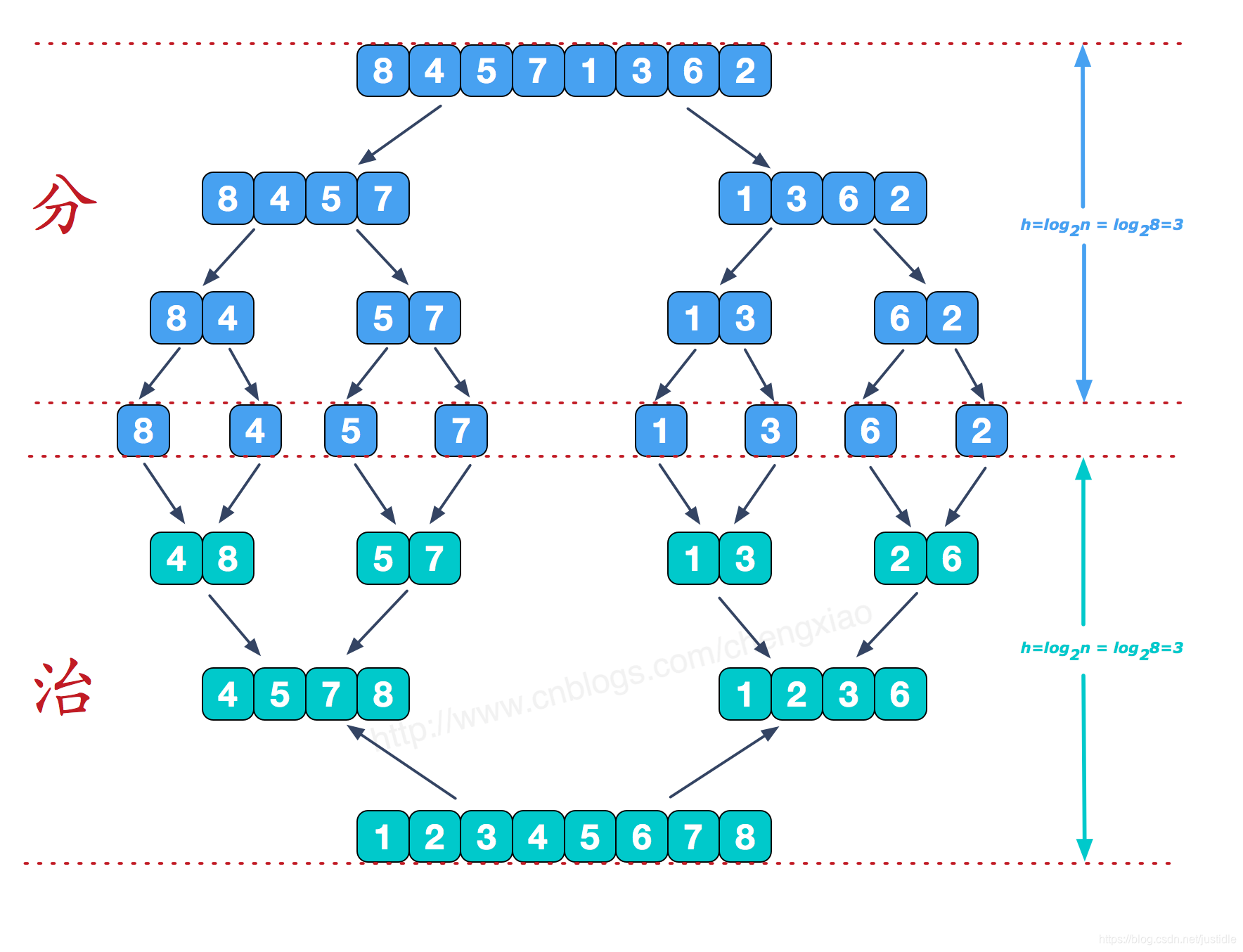
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
合并两个有序数组流程
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
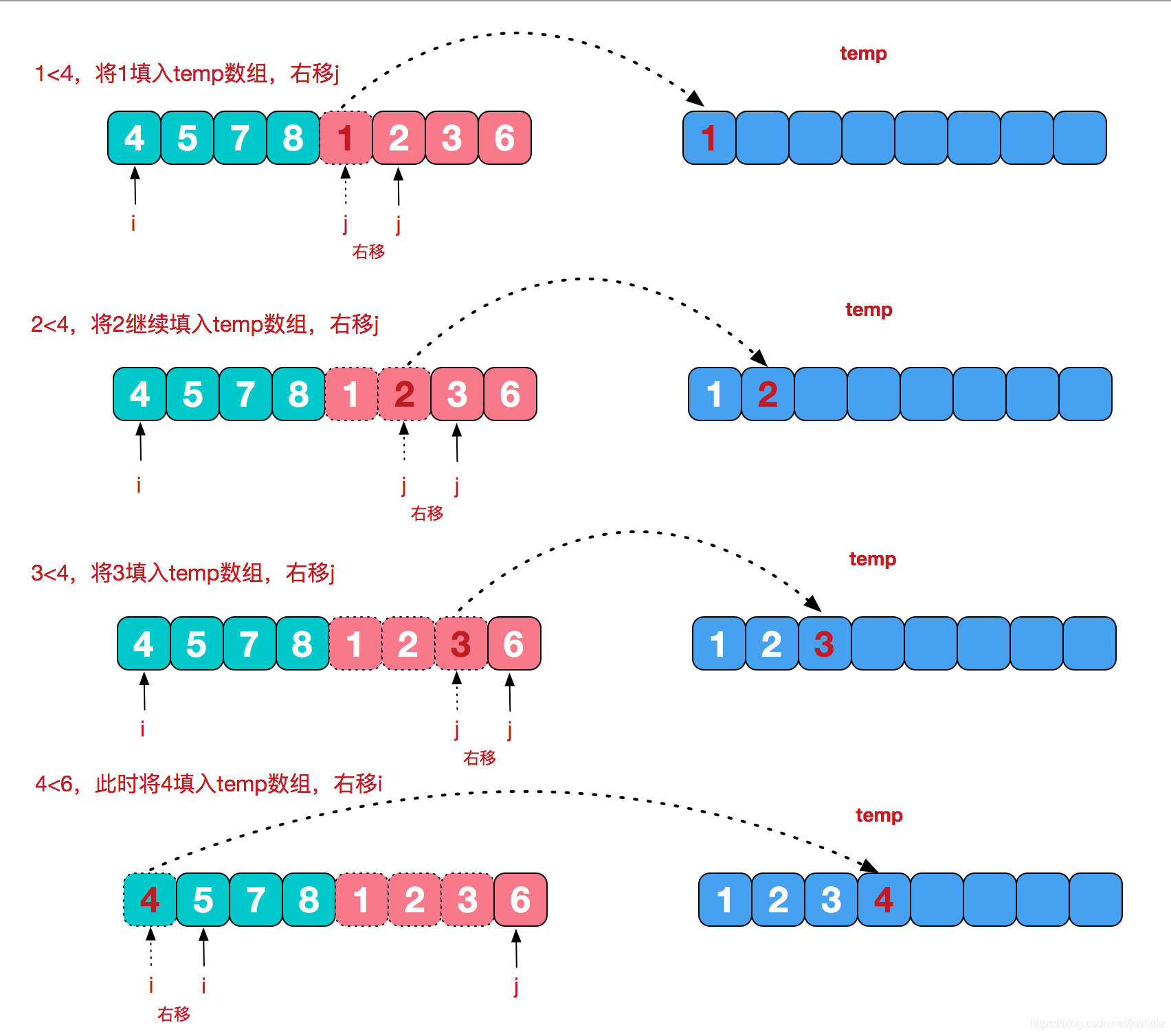
动画展示
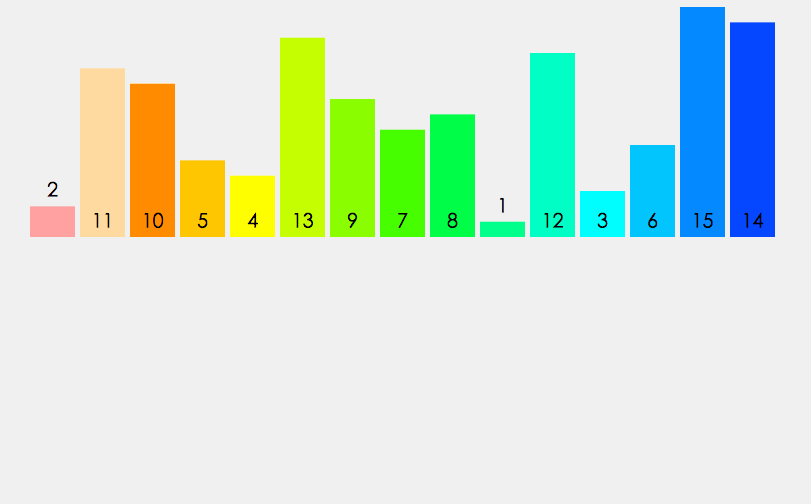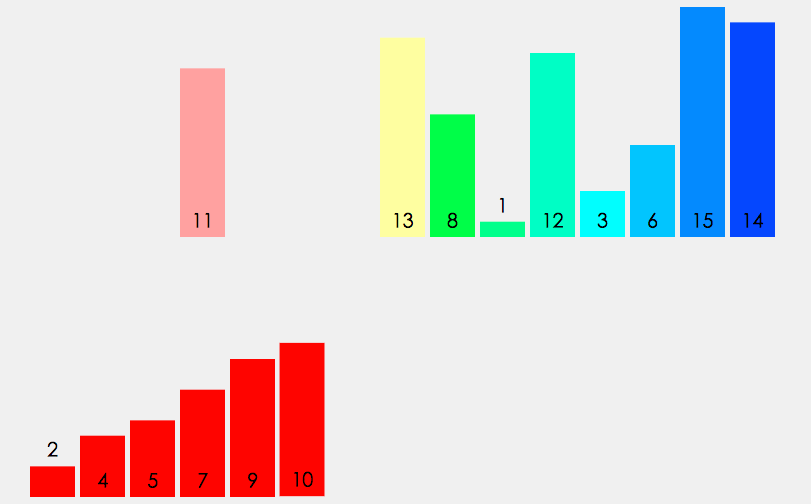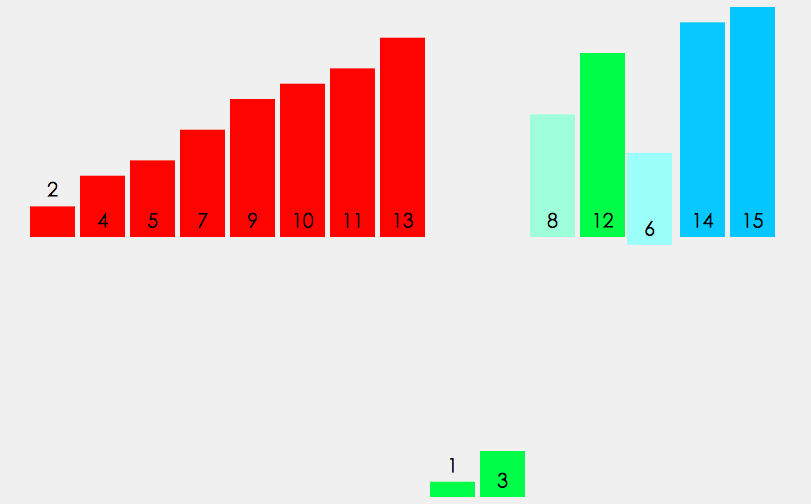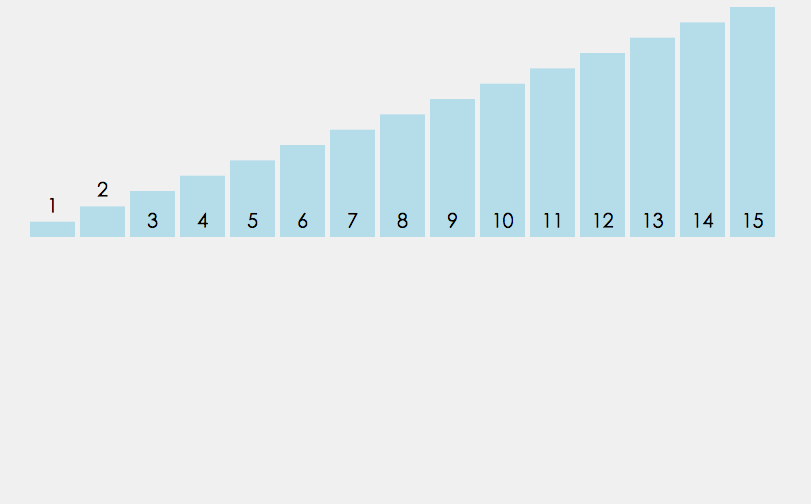
算法性能
速度仅次于快速排序。
时间复杂度
O(nlogn)。
空间复杂度
O(N),归并排序需要一个与原数组相同长度的数组做辅助来排序。
稳定性
稳定。
代码实现
# 定义归并排序函数
def MergeSort(lists):
# 如果列表长度小于或等于1,直接返回列表,因为它已经是有序的
if len(lists) <= 1:
return lists
# 计算列表的中间位置
num = int(len(lists) / 2)
# 对列表的前半部分进行归并排序
left = MergeSort(lists[:num])
# 对列表的后半部分进行归并排序
right = MergeSort(lists[num:])
# 合并排序好的两个半部分
return Merge(left, right)
# 定义合并两个有序列表的函数
def Merge(left, right):
# 初始化两个指针,分别指向两个列表的起始位置
r, l = 0, 0
# 初始化结果列表
result = []
# 当两个列表都有元素时,进行比较和合并
while l < len(left) and r < len(right):
# 如果左列表当前元素小于等于右列表当前元素,将左列表元素添加到结果列表
if left[l] <= right[r]:
result.append(left[l])
l += 1
# 否则,将右列表元素添加到结果列表
else:
result.append(right[r])
r += 1
# 将左列表剩余的所有元素添加到结果列表
result += list(left[l:])
# 将右列表剩余的所有元素添加到结果列表
result += list(right[r:])
# 返回合并后的有序列表
return result
# 测试归并排序函数
print(MergeSort([1, 2, 3, 4, 5, 6, 7, 90, 21, 23, 45]))运行结果:
[1, 2, 3, 4, 5, 6, 7, 21, 23, 45, 90]






Comments NOTHING